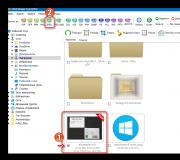
Oplossing volgens de Jordan Gauss-methode. Gauss-Jordan-methode
Gauss-Jordan-methode. Hoe te vinden omgekeerde matrix
door te gebruiken elementaire transformaties?
Er was eens de Duitse wiskundige Wilhelm Jordan (we transcriberen verkeerd vanuit het DuitsJordanië als Jordanië) ging zitten om een ander stelsel vergelijkingen op te lossen. Hij deed dit graag en vrije tijd verbeterde zijn vaardigheden. Maar toen kwam het moment dat hij zich verveelde met alle methoden om problemen op te lossen en Gaussische methode inbegrepen...
Stel dat we een systeem krijgen met drie vergelijkingen, drie onbekenden, en de uitgebreide matrix ervan wordt opgeschreven. In het meest voorkomende geval krijgt u standaardstappen, enzovoort, elke dag... Hetzelfde: als hopeloze novemberregen.
Verdrijft de melancholie voor een tijdje een andere manier de matrix in een getrapte vorm brengen: , en het is volledig gelijkwaardig en kan alleen lastig zijn vanwege subjectieve perceptie. Maar vroeg of laat wordt alles saai... En toen dacht ik O rdan - waarom zou je je überhaupt druk maken over de omgekeerde beweging van het Gauss-algoritme? Is het niet gemakkelijker om het antwoord onmiddellijk te krijgen met behulp van aanvullende elementaire transformaties?
...ja, dit gebeurt alleen uit liefde =)
Onder de knie krijgen deze les“dummies” zullen de F-weg moeten volgen O rdan en upgrade elementaire transformaties naar minimaal een gemiddeld niveau, nadat je minimaal 15-20 relevante taken hebt voltooid. Daarom, als u vaag begrijpt waar het gesprek over gaat en/of als u tijdens de les iets verkeerd begrijpt, raad ik u aan om in de volgende volgorde vertrouwd te raken met het onderwerp:
Nou, het is absoluut geweldig als het lukt het reduceren van de volgorde van de determinant.
Zoals iedereen begrijpt is de Gauss-Jordan-methode een aanpassing Gauss-methode en we zullen de implementatie van het hoofdidee dat hierboven al is geuit op de dichtstbijzijnde schermen ontmoeten. Daarnaast is een van de weinige voorbeelden in dit artikel opgenomen kritische toepassing – het vinden van de inverse matrix met behulp van elementaire transformaties.
Zonder verder oponthoud:
Voorbeeld 1
Los het systeem op met behulp van de Gauss-Jordan-methode 
Oplossing: dit is de eerste taak van de les Gaussiaanse methode voor dummies, waar we de uitgebreide matrix van het systeem 5 keer hebben getransformeerd en naar een stapsgewijze vorm hebben gebracht: 
Nu in plaats daarvan achteruit Bijkomende elementaire transformaties spelen een rol. Eerst moeten we op deze plaatsen nullen krijgen:  ,
,
en dan nog een nul hier:  .
.
Een ideaal geval vanuit het oogpunt van eenvoud:
(6) Aan de tweede regel is een derde regel toegevoegd. Er werd een derde regel aan de eerste regel toegevoegd.
(7) De tweede regel werd opgeteld bij de eerste regel, vermenigvuldigd met –2.
Ik kan het niet helpen, maar illustreer het uiteindelijke systeem: 
Antwoord: ![]()
Ik waarschuw lezers ervoor om niet in een ondeugende bui te zijn - dit was een eenvoudig demonstratievoorbeeld. De Gauss-Jordan-methode heeft zijn eigen specifieke technieken en niet de handigste berekeningen, dus bereid je voor op serieus werk.
Ik wil niet categorisch of kieskeurig lijken, maar in de overgrote meerderheid van de informatiebronnen die ik heb gezien, typische taken worden als extreem slecht beschouwd - je moet slim zijn en veel tijd/zenuwen besteden aan een moeilijke, onhandige oplossing met breuken. Door de jaren heen ben ik erin geslaagd om te polijsten, ik zal niet zeggen dat dit de beste is, maar een rationele en redelijk gemakkelijke techniek die beschikbaar is voor iedereen die het weet rekenkundige bewerkingen:
Voorbeeld 2
Los het systeem op lineaire vergelijkingen Gauss-Jordan-methode. 
Oplossing: Het eerste deel van de taak is heel bekend: 
(1) De eerste regel is opgeteld bij de tweede regel, vermenigvuldigd met –1. De eerste regel, vermenigvuldigd met 3, werd toegevoegd aan de derde regel. De eerste regel, vermenigvuldigd met –5, werd toegevoegd aan de vierde regel.
(2) De tweede regel is gedeeld door 2, de derde regel is gedeeld door 11, de vierde regel is gedeeld door 3.
(3) De tweede en derde regel zijn proportioneel, de derde regel is verwijderd. Er werd een tweede regel toegevoegd aan de vierde regel, vermenigvuldigd met –7
(4) De derde regel werd gedeeld door 2.
Het is duidelijk dat het systeem oneindig veel oplossingen heeft, en het is onze taak om de uitgebreide matrix ervan in de vorm te brengen  .
.
Hoe verder? Allereerst moet worden opgemerkt dat we een smakelijke elementaire transformatie verloren hebben: herschikking van snaren. Om precies te zijn, het is mogelijk om ze te herschikken, maar dit heeft geen zin (we zullen eenvoudigweg onnodige acties uitvoeren). En dan is het raadzaam om het volgende sjabloon te volgen:
Wij vinden kleinste gemene veelvoud getallen in de derde kolom (1, –1 en 3), d.w.z. – het kleinste getal dat zonder rest deelbaar zou zijn door 1, –1 en 3. in dit geval, dit is natuurlijk een “drie”. Nu in de derde kolom moeten we getallen krijgen die identiek zijn in modulus, en deze overwegingen bepalen de 5e transformatie van de matrix:
(5) We vermenigvuldigen de eerste regel met –3, vermenigvuldigen de tweede regel met 3. Over het algemeen zou de eerste regel ook met 3 kunnen worden vermenigvuldigd, maar dit zou minder handig zijn voor de volgende actie. Je raakt snel gewend aan goede dingen:

(6) Aan de tweede regel is een derde regel toegevoegd. Er werd een derde regel aan de eerste regel toegevoegd.
(7) De tweede kolom heeft twee waarden die niet nul zijn (24 en 6) en opnieuw moeten we deze verkrijgen getallen identiek in modulus. In dit geval is alles redelijk goed gelukt: het kleinste veelvoud van 24, en het is het meest effectief om de tweede regel met -4 te vermenigvuldigen.
(8) Er is een tweede regel toegevoegd aan de eerste regel.
(9) Final touch: de eerste lijn wordt gedeeld door -3, de tweede lijn wordt gedeeld door -24 en de derde lijn wordt gedeeld door 3. Deze actie wordt uitgevoerd LAATSTE KEER! Geen voortijdige breuken!
Als resultaat van elementaire transformaties werd een gelijkwaardig origineel systeem verkregen: 
We drukken de basisvariabelen eenvoudigweg uit in termen van de vrije variabele: 
en schrijf:
Antwoord: algemene oplossing: ![]()
In dergelijke voorbeelden is het gebruik van het beschouwde algoritme meestal gerechtvaardigd, omdat het omgekeerde het geval is Gauss-methode vereist meestal tijdrovende en frustrerende berekeningen met breuken.
En het is natuurlijk zeer wenselijk om dit te controleren, wat wordt uitgevoerd volgens het gebruikelijke schema dat in de les wordt besproken Incompatibele systemen en systemen met een gemeenschappelijke oplossing.
Voor onafhankelijke beslissing:
Voorbeeld 3
Vind een basisoplossing met behulp van elementaire transformaties 
Deze formulering van het probleem veronderstelt het gebruik van de Gauss-Jordan-methode, en in de voorbeeldoplossing wordt de matrix gereduceerd tot standaard weergave  met basisvariabelen. Houd daar echter altijd rekening mee U kunt andere variabelen als basisvariabelen kiezen. Dus als de eerste kolom bijvoorbeeld lastige getallen bevat, is het heel acceptabel om de matrix tot de vorm terug te brengen
met basisvariabelen. Houd daar echter altijd rekening mee U kunt andere variabelen als basisvariabelen kiezen. Dus als de eerste kolom bijvoorbeeld lastige getallen bevat, is het heel acceptabel om de matrix tot de vorm terug te brengen  (basisvariabelen), of naar het formulier
(basisvariabelen), of naar het formulier  (basisvariabelen), of zelfs naar het formulier
(basisvariabelen), of zelfs naar het formulier  met basisvariabelen. Er zijn andere opties.
met basisvariabelen. Er zijn andere opties.
Maar toch zijn dit extreme gevallen - het is niet nodig om leraren opnieuw te choqueren met je kennis, oplossingstechniek, en nog meer, het is niet nodig om exotische Jordan-resultaten te produceren zoals  . Het kan echter moeilijk zijn om weerstand te bieden aan het gebruik van een atypische basis wanneer de oorspronkelijke matrix, bijvoorbeeld in de vierde kolom, twee kant-en-klare nullen heeft.
. Het kan echter moeilijk zijn om weerstand te bieden aan het gebruik van een atypische basis wanneer de oorspronkelijke matrix, bijvoorbeeld in de vierde kolom, twee kant-en-klare nullen heeft.
Opmerking : de term “basis” heeft een algebraïsche betekenis en concept geometrische basis heeft er niets mee te maken!
Als in de uitgebreide matrix van gegevensgroottes plotseling een paar wordt ontdekt lineair afhankelijk lijnen, dan moet je proberen het terug te brengen tot vertrouwde uitstraling  met basisvariabelen. Een voorbeeld van een dergelijke beslissing staat in voorbeeld nr. 7 van het artikel over homogene systemen van lineaire vergelijkingen, en daar er wordt een andere basis gekozen.
met basisvariabelen. Een voorbeeld van een dergelijke beslissing staat in voorbeeld nr. 7 van het artikel over homogene systemen van lineaire vergelijkingen, en daar er wordt een andere basis gekozen.
De volgende keer blijven we onze vaardigheden verbeteren toegepast probleem:
Hoe vind je de inverse matrix met behulp van de Gauss-methode?
Meestal wordt de voorwaarde afgekort geformuleerd, maar in essentie werkt ook hier het Gauss-Jordan-algoritme. Een eenvoudigere manier van vinden omgekeerde matrix voor een vierkante matrix hebben we er lang geleden in de bijbehorende les naar gekeken, en in de barre late herfst beheersen doorgewinterde studenten een meesterlijke methode om het op te lossen.
Samenvatting komende acties zijn als volgt: eerst moet je opschrijven vierkante matrix in combinatie met de identiteitsmatrix: . Vervolgens is het met behulp van elementaire transformaties nodig om de identiteitsmatrix aan de linkerkant te verkrijgen, while (zonder op theoretische details in te gaan) de inverse matrix wordt aan de rechterkant getekend. Schematisch ziet de oplossing er als volgt uit:
![]()
(Het is duidelijk dat de inverse matrix moet bestaan)
Demonstratie 4
Laten we de inverse matrix voor een matrix vinden met behulp van elementaire transformaties. Om dit te doen, schrijven we het in één harnas met de identiteitsmatrix, en de “twee paarden” snelt weg:
(1) De eerste regel is opgeteld bij de tweede regel, vermenigvuldigd met –3.
(2) Er is een tweede regel toegevoegd aan de eerste regel.
(3) De tweede regel werd gedeeld door –2.
Antwoord: ![]()
Controleer het antwoord in de eerste voorbeeldles Hoe vind je de inverse van een matrix?
Maar het was gewoon weer een verleidelijk probleem - in werkelijkheid is de oplossing veel tijdrovender en moeizamer. Normaal gesproken krijgt u een matrix van drie bij drie te zien:
Voorbeeld 5

Oplossing: we voegen de identiteitsmatrix toe en beginnen transformaties uit te voeren, waarbij we ons houden aan het ‘gebruikelijke’ algoritme Gauss-methode:
(1) De eerste en derde regel zijn verwisseld. Op het eerste gezicht lijkt het herschikken van rijen illegaal, maar in feite is het mogelijk om ze te herschikken - als gevolg daarvan moeten we aan de linkerkant de identiteitsmatrix krijgen, en aan de rechterkant zullen we precies de matrix "forceren" (ongeacht of we de lijnen tijdens de oplossing herschikken of niet). Houd er rekening mee dat u hier, in plaats van permutatie, “zessen” in de eerste kolom kunt plaatsen (kleinste gemene veelvoud (LCM) van 3, 2 en 1). De LCM-oplossing is vooral handig als er geen “eenheden” in de eerste kolom staan.
(2) De eerste regel is toegevoegd aan de tweede en derde regel, respectievelijk vermenigvuldigd met –2 en –3.
(3) De tweede regel is toegevoegd aan de derde regel, vermenigvuldigd met –1
Het tweede deel van de oplossing wordt uitgevoerd volgens het schema dat al bekend is uit de vorige paragraaf: permutaties van rijen worden betekenisloos en we vinden het kleinste gemene veelvoud van de getallen in de derde kolom (1, –5, 4): 20 Er is een strikt algoritme voor het vinden van de LCM, maar selectie is hier meestal voldoende. Het is prima als je een groter getal neemt dat deelbaar is door 1, -5 en 4, bijvoorbeeld het getal 40. Het verschil zit in omslachtiger berekeningen.
Over berekeningen gesproken. Om dit probleem op te lossen, is het geen schande om jezelf te bewapenen met een microcalculator - er zijn hier veel getallen bij betrokken, en het zou zeer teleurstellend zijn als je een rekenfout maakt.
(4) Vermenigvuldig de derde regel met 5, de tweede regel met 4, de eerste regel met “min twintig”:

(5) Er is een derde regel toegevoegd aan de 1e en 2e regel.
(6) De eerste en derde regel werden gedeeld door 5, de tweede regel werd vermenigvuldigd met –1.
(7) Het kleinste gemene veelvoud van de getallen die niet nul zijn in de tweede kolom (–20 en 44) is 220. Vermenigvuldig de eerste rij met 11, de tweede rij met 5.
(8) Er is een tweede regel toegevoegd aan de eerste regel.
(9) De eerste regel werd vermenigvuldigd met –1, de tweede regel werd “terug” gedeeld door 5.
(10) Nu op de hoofddiagonaal van de linkermatrix is het raadzaam om te verkrijgen kleinste gemene veelvoud van diagonale getallen (44, 44 en 4). Het is volkomen duidelijk dat dit getal 44 is. We vermenigvuldigen de derde regel met 11.
(11) Deel elke lijn door 44. Deze actie laatste gedaan!
De inverse matrix is dus: 
Het invoegen en verwijderen hiervan zijn in principe onnodige handelingen, maar dit is wel vereist door het taakregistratieprotocol.
Antwoord: 
De controle wordt uitgevoerd volgens het gebruikelijke schema dat in de les wordt besproken omgekeerde matrix.
Gevorderde mensen kunnen de oplossing enigszins inkorten, maar ik moet u waarschuwen dat haast hier gepaard gaat met een VERHOOGD risico om een fout te maken.
Een soortgelijke taak voor een onafhankelijke oplossing:
Voorbeeld 6
Vind de inverse matrix met behulp van de Gauss-Jordan-methode. 
Een voorbeeld van een taak bij benadering onderaan de pagina. En zodat je "niet rijdt door te zingen", heb ik de oplossing in de reeds genoemde stijl ontworpen - uitsluitend via de LCM van kolommen zonder een enkele herschikking van rijen en extra kunstmatige transformaties. Naar mijn mening, dit schema is, zo niet het meest, dan wel een van de meest betrouwbare.
Soms is een kortere ‘modernistische’ oplossing handig, namelijk als volgt: in de eerste stap is alles zoals gewoonlijk:  .
.
Bij de tweede stap worden, met behulp van een beproefde techniek (via de LCM van getallen in de tweede kolom), twee nullen tegelijk in de tweede kolom georganiseerd:  . Het is vooral moeilijk om deze actie te weerstaan als er in de tweede kolom getallen met dezelfde absolute waarde staan, bijvoorbeeld dezelfde banale 'eenheden'.
. Het is vooral moeilijk om deze actie te weerstaan als er in de tweede kolom getallen met dezelfde absolute waarde staan, bijvoorbeeld dezelfde banale 'eenheden'.
En tenslotte, in de derde stap, komen we op precies dezelfde manier terecht noodzakelijke nullen in de derde kolom:  .
.
Wat de dimensie betreft, is het in de meeste gevallen noodzakelijk om de matrix "drie bij drie" op te lossen. Van tijd tot tijd is er echter een lichte versie van het probleem met een “twee bij twee” matrix en een harde... - een website speciaal voor alle lezers:
Voorbeeld 7
Vind de inverse van een matrix met behulp van elementaire transformaties 
Dit is een opdracht van mijn eigen Natuurkunde en Wiskunde proefwerk in algebra, ...oh, waar is mijn eerste cursus =) Vijftien jaar geleden (het blad is verrassend genoeg nog niet geel geworden), Ik deed het in 8 stappen, maar nu zijn het er nog maar 6! De matrix is trouwens erg creatief: bij de allereerste stap zijn verschillende verleidelijke oplossingen zichtbaar. Mijn latere versie onderaan de pagina.
En het laatste advies - na dergelijke voorbeelden, ooggymnastiek en een soort van goede muziek voor ontspanning =)
Ik wens je succes!
Oplossingen en antwoorden:
Voorbeeld 3: Oplossing: we schrijven de uitgebreide matrix van het systeem op en verkrijgen, met behulp van elementaire transformaties, de basisoplossing:
(1) De eerste en tweede regel zijn verwisseld.
(2) De eerste regel is opgeteld bij de tweede regel, vermenigvuldigd met –2. De eerste regel werd toegevoegd aan de derde regel, vermenigvuldigd met 5.
(3) De derde regel werd gedeeld door 3.
(4) De tweede regel werd opgeteld bij de derde regel, vermenigvuldigd met 2.
(5) De derde regel werd gedeeld door 7.
(6) Het kleinste veelvoud van de getallen in de 3e kolom (–3, 5, 1) is 15. De eerste rij wordt vermenigvuldigd met 5, de tweede rij wordt vermenigvuldigd met –3, de derde rij wordt vermenigvuldigd met 15.
(7) Er is een derde regel toegevoegd aan de eerste regel. Aan de tweede regel werd een 3e regel toegevoegd.
(8) De eerste regel werd gedeeld door 5, de tweede regel werd gedeeld door –3, de derde regel werd gedeeld door 15.
(9) Het kleinste veelvoud van de getallen die niet nul zijn in de 2e kolom (–2 en 1) is gelijk aan: 2. De tweede rij is vermenigvuldigd met 2
(10) Er is een tweede regel toegevoegd aan de eerste regel.
(11) De tweede regel werd gedeeld door 2.
Laten we de basisvariabelen uitdrukken in termen van vrije variabelen:
Antwoord
: algemene oplossing:
Voorbeeld 6: Oplossing: we vinden de inverse matrix met behulp van elementaire transformaties:
(1) De eerste regel werd vermenigvuldigd met –15, de tweede regel werd vermenigvuldigd met 3, de derde regel werd vermenigvuldigd met 5.
(2) De eerste regel is toegevoegd aan de 2e en 3e regel.
(3) De eerste regel werd gedeeld door –15, de tweede regel werd gedeeld door –3, de derde regel werd gedeeld door –5.
(4) De tweede regel werd vermenigvuldigd met 7, de derde regel werd vermenigvuldigd met –9.
(5) Er is een tweede regel toegevoegd aan de derde regel.
(6) De tweede regel werd gedeeld door 7.
(7) De eerste regel werd vermenigvuldigd met 27, de tweede regel werd vermenigvuldigd met 6, de derde regel werd vermenigvuldigd met –4.
(8) Er is een derde regel toegevoegd aan de eerste en tweede regel.
(9) De derde regel werd gedeeld door –4. De tweede regel werd opgeteld bij de eerste regel, vermenigvuldigd met –1.
(10) De tweede regel werd gedeeld door 2.
(11) Elke lijn werd gedeeld door 27.
Als resultaat: 
Antwoord
: 
Voorbeeld 7: Oplossing: laten we de inverse matrix vinden met behulp van de Gauss-Jordan-methode:
(1) Er is een derde regel toegevoegd aan de eerste en vierde regel.
(2) De eerste en vierde regel zijn verwisseld.
(3) De eerste regel is toegevoegd aan de tweede regel. De 1e regel is toegevoegd aan de 3e regel, vermenigvuldigd met 2:
(4) De tweede regel is toegevoegd aan de derde regel, vermenigvuldigd met –2. Er is een 2e regel toegevoegd aan de 4e regel.
(5) De 4e regel werd opgeteld bij de 1e en 3e regel, vermenigvuldigd met –1.
(6) De tweede regel werd vermenigvuldigd met –1, de derde regel werd gedeeld door –2.
Antwoord
: 
De Gauss-Jordan-methode is ontworpen om lineaire systemen op te lossen algebraïsche vergelijkingen(SLAU). Het is een wijziging van de Gauss-methode. Als de Gauss-methode in twee fasen wordt uitgevoerd (vooruit en achteruit), kunt u met de Gauss-Jordan-methode het systeem in één fase oplossen. Details en directe toepassing van de Gauss-Jordan-methode worden in de voorbeelden beschreven.
In alle voorbeelden geeft $A$ de systeemmatrix aan, $\widetilde(A)$ de uitgebreide systeemmatrix. U kunt lezen over de matrixvorm van het opnemen van SLAE.
Voorbeeld nr. 1
Los SLAE $ \left\( \begin(uitgelijnd) & 4x_1-7x_2+8x_3=-23;\\ & 2x_1-4x_2+5x_3=-13;\\ & -3x_1+11x_2+x_3=16 op. \end(uitgelijnd ) \right.$ volgens de Gauss-Jordan-methode.
Laten we van de laatste matrix die we hebben ontvangen naar het systeem gaan:
$$ \left\( \begin(uitgelijnd) & 0\cdot x_1+1\cdot x_2+0\cdot x_3=1;\\ & 1\cdot x_1+0\cdot x_2+0\cdot x_3=-2; \\ & 0\cdot x_1+0\cdot x_2+1\cdot x_3=-1 \end(uitgelijnd) \right $$.
Als we het resulterende systeem vereenvoudigen, hebben we:
$$ \left\( \begin(uitgelijnd) & x_2=1;\\ & x_1=-2;\\ & x_3=-1. \end(uitgelijnd) \right. $$
Volledige oplossing zonder uitleg ziet het er zo uit:

Hoewel deze methode voor het selecteren van oplossende elementen zeer acceptabel is, verdient het de voorkeur om diagonale elementen van de systeemmatrix als oplossende elementen te selecteren. We zullen deze methode hieronder bekijken.
Selectie van oplossende elementen op de hoofddiagonaal van de systeemmatrix.
Omdat deze oplossingsmethode volledig vergelijkbaar is met de vorige (behalve de selectie van inschakelelementen), slaan we gedetailleerde uitleg over. Het principe van het selecteren van activerende elementen is eenvoudig: in de eerste kolom selecteren we het element van de eerste rij, in de tweede kolom nemen we het element van de tweede rij, in de derde kolom nemen we het element van de derde rij, enzovoort. op.
Eerste stap
Selecteer in de eerste kolom het element van de eerste rij, d.w.z. we hebben element 4 als oplossend element. Ik begrijp dat het kiezen van nummer 2 de voorkeur verdient, aangezien dit getal nog steeds kleiner is dan 4. Laten we, om ervoor te zorgen dat nummer 2 in de eerste kolom naar de eerste plaats gaat, het eerste omwisselen. en tweede rijen:
$$ \left(\begin(matrix) (ccc|c) 4 & -7 & 8 & -23\\ 2 & -4& 5 & -13 \\ -3 & 11 & 1 & 16 \end(matrix) \ rechts)\pijl rechts \left(\begin(matrix) (ccc|c) 2 & -4& 5 & -13\\ 4 & -7 & 8 & -23 \\ -3 & 11 & 1 & 16 \end(matrix ) \rechts)$$
Het inschakelelement wordt dus weergegeven door het getal 2. Deel op dezelfde manier als voorheen de eerste rij door 2 en zet vervolgens de elementen van de eerste kolom terug op nul:
$$ \left(\begin(matrix) (ccc|c) 2 & -4& 5 & -13\\ 4 & -7 & 8 & -23 \\ -3 & 11 & 1 & 16 \end(matrix) \ rechts) \begin(array) (l) I:2 \\\phantom(0) \\ \phantom(0) \end(array) \rightarrow \left(\begin(array) (ccc|c) 1 & - 2& 5/2 & -13/2 \\4 & -7 & 8 & -23\\ -3 & 11 & 1 & 16 \end(array) \right) \begin(array) (l) \phantom(0 ) \\ II-4\cdot I\\ III+3\cdot I \end(array) \rightarrow \left(\begin(array) (ccc|c) 1 & -2& 5/2 & -13/2\ \0 & 1 & -2 & 3\\ 0 & 5 & 17/2 & -7/2 \end(array) \right). $$
Tweede stap
De tweede stap vereist het op nul zetten van de elementen van de tweede kolom. We selecteren het element van de tweede regel als het oplossende element, d.w.z. 1. Het activeringselement is al aanwezig gelijk aan één, dus we zullen geen regels verwisselen. Als we rijen zouden willen verwisselen, zouden we trouwens de eerste rij niet aanraken, omdat deze al in de eerste stap werd gebruikt. Maar de tweede en derde regel kunnen eenvoudig worden verwisseld. Ik herhaal echter dat het in deze situatie niet nodig is om de rijen te verwisselen, omdat het oplossende element al optimaal is: het is gelijk aan één.
$$ \left(\begin(matrix) (ccc|c) 1 & -2& 5/2 & -13/2\\0 & 1 & -2 & 3\\ 0 & 5 & 17/2 & -7/ 2 \end(array) \right) \begin(array) (l) I+2\cdot II \\ \phantom(0)\\ III-5\cdot II \end(array) \rightarrow \left(\begin (array) (ccc|c) 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 37/2 & -37/2 \end(array) \rechts). $$
De tweede stap is voltooid. Laten we verder gaan met de derde stap.
Derde stap
De derde stap vereist het op nul zetten van de elementen van de derde kolom. Als oplossend element selecteren we het element van de derde regel, d.w.z. 37/2. Verdeel de elementen van de derde rij door 37/2 (zodat het oplossende element gelijk wordt aan 1) en zet vervolgens de overeenkomstige elementen van de derde kolom terug op nul:
$$ \left(\begin(array) (ccc|c) 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 37/2 & -37 /2 \end(array) \right) \begin(array) (l) \phantom(0)\\ \phantom(0)\\ III:\frac(37)(2) \end(array) \pijl naar rechts \ left(\begin(matrix) (ccc|c) 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 1 & -1 \end(matrix) \right) \begin(array) (l) I+2\cdot III\\II+3/2\cdot III\\ \phantom(0) \end(array) \rightarrow \left(\begin(array) ( ccc|c) 1 & 0 & 0 & -2 \\ 0 & 1 & 0 & 1\\ 0 & 0 & 1 & -1 \end(array) \right). $$
Ontvangen antwoord: $x_1=-2$, $x_2=1$, $x_3=-1$. De volledige oplossing zonder uitleg ziet er als volgt uit:

Alle andere voorbeelden op deze pagina zullen precies op de tweede manier worden opgelost: we zullen diagonale elementen van de systeemmatrix selecteren als oplossende elementen.
Antwoord: $x_1=-2$, $x_2=1$, $x_3=-1$.
Voorbeeld nr. 2
SLAE $ \left\( \begin(uitgelijnd) & 3x_1+x_2+2x_3+5x_4=-6;\\ & 3x_1+x_2+2x_4=-10;\\ & 6x_1+4x_2+11x_3+11x_4=-27; \\ & -3x_1-2x_2-2x_3-10x_4=1 \end(uitgelijnd) \right.$ volgens de Gauss-Jordan-methode.
Laten we de uitgebreide matrix van dit systeem schrijven: $\widetilde(A)=\left(\begin(array) (cccc|c) 3 & 1 & 2 & 5 & -6\\ 3 & 1& 0 & 2 & -10 \\ 6 & 4 & 11 & 11 & -27 \\ -3 & -2 & -2 & -10 & 1 \end(array) \right)$.
We zullen diagonale elementen van de systeemmatrix selecteren als oplossende elementen: bij de eerste stap nemen we het element van de eerste rij, bij de tweede stap nemen we het element van de tweede rij, enzovoort.
Eerste stap
We moeten de overeenkomstige elementen van de eerste kolom opnieuw instellen op nul. Laten we het element van de eerste regel als een oplossend element nemen, d.w.z. 3. Dienovereenkomstig zal de eerste regel door 3 moeten worden gedeeld, zodat het oplossende element gelijk wordt aan één. En reset vervolgens alle elementen van de eerste kolom, behalve de toegestane:
$$ \left(\begin(array)(cccc|c) 3 & 1 & 2 & 5 & -6\\ 3 & 1 & 0 & 2 & -10\\ 6 & 4 & 11 & 11 & -27\ \ -3 & -2 & -2 & -10 & 1\end(array)\right) \begin(array) (l) I:3\\ \phantom(0)\\\phantom(0)\\\ phantom(0)\end(array) \pijl naar rechts \left(\begin(array)(cccc|c) 1 & 1/3 & 2/3 & 5/3 & -2\\ 3 & 1 & 0 & 2 & -10\\ 6 & 4 & 11 & 11 & -27\\ -3 & -2 & -2 & -10 & 1\end(array)\right) \begin(array) (l) \phantom(0) \\ II-3\cdot I\\III-6\cdot I\\IV+3\cdot I\end(array) \rightarrow\\ \rightarrow\left(\begin(array)(cccc|c) 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & 0 & -2 & -3 & -4\\ 0 & 2 & 7 & 1 & -15\\ 0 & -1 & 0 & - 5 & -5\end(matrix)\rechts). $$
Tweede stap
We gaan verder met het op nul zetten van de overeenkomstige elementen van de tweede kolom. We hebben afgesproken om het element van de tweede lijn als oplossend element te nemen, maar sindsdien kunnen we dit niet meer doen vereist onderdeel gelijk aan nul. Conclusie: we zullen de lijnen verwisselen. De eerste regel kan niet worden aangeraakt, omdat deze al in de eerste stap werd gebruikt. De keuze is niet rijk: we wisselen de tweede en derde regel om, of we wisselen de vierde en tweede regel om. Omdat de vierde regel (-1) bevat, laat dan de vierde regel deelnemen aan de “uitwisseling”. Wissel dus de tweede en vierde regel om:
$$ \left(\begin(matrix)(cccc|c) 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & 0 & -2 & -3 & -4\\ 0 & 2 & 7 & 1 & -15\\ 0 & -1 & 0 & -5 & -5\end(array)\right)\pijl rechts \left(\begin(array)(cccc|c) 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & -1 & 0 & -5 & -5\\ 0 & 2 & 7 & 1 & -15\\ 0 & 0 & -2 & -3 & -4 \end(array)\right) $$
Nu is alles normaal: het resolutie-element is gelijk aan (-1). Het komt overigens voor dat het veranderen van de posities van lijnen onmogelijk is, maar we zullen dit in het volgende voorbeeld nr. 3 bespreken. Voorlopig delen we de tweede rij door (-1) en resetten we vervolgens de elementen van de tweede kolom. Houd er rekening mee dat in de tweede kolom het element in de vierde rij al gelijk is aan nul, dus we zullen de vierde rij niet aanraken.
$$ \left(\begin(matrix)(cccc|c) 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & -1 & 0 & -5 & -5\\ 0 & 2 & 7 & 1 & -15\\ 0 & 0 & -2 & -3 & -4\end(array)\right) \begin(array) (l) \phantom(0)\\II:(-1) \\\phantom(0)\\\phantom(0)\end(array) \rightarrow \left(\begin(array)(cccc|c) 1 & 1/3 & 2/3 & 5/3 & -2 \\ 0 & 1 & 0 & 5 & 5\\ 0 & 2 & 7 & 1 & -15\\ 0 & 0 & -2 & -3 & -4\end(matrix)\right) \begin(matrix) (l) I-1/3\cdot II\\ \phantom(0) \\III-2\cdot II\\\phantom(0)\end(array) \rightarrow\\ \rightarrow\left(\begin( array)(cccc|c) 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 7 & -9 & -25\\ 0 & 0 & -2 & -3 & -4\end(matrix)\rechts). $$
Derde stap
Laten we beginnen met het verwerken van de derde kolom. We hebben afgesproken om de diagonale elementen van de systeemmatrix als oplossend element te nemen. Voor de derde stap betekent dit het selecteren van het element op de derde rij. Als we echter simpelweg element 7 als oplossend element nemen, dan zal de gehele derde regel door 7 moeten worden gedeeld. Het lijkt mij dat delen door (-2) eenvoudiger is. Laten we daarom de derde en vierde regel verwisselen, en dan wordt het oplossende element (-2):
$$ \left(\begin(matrix)(cccc|c) 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 7 & -9 & -25\\ 0 & 0 & -2 & -3 & -4\end(array)\right) \pijl rechts \left(\begin(array)(cccc|c) 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & -2 & -3 & -4\\ 0 & 0 & 7 & -9 & -25\end(array)\right) $$
Resolutie-element - (-2). Deel de derde rij door (-2) en reset de overeenkomstige elementen van de derde kolom:
$$ \left(\begin(matrix)(cccc|c) 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & -2 & - 3 & -4\\ 0 & 0 & 7 & -9 & -25\end(array)\right) \begin(array) (l) \phantom(0)\\ \phantom(0) \\III:( -2)\\\phantom(0)\end(array)\rightarrow \left(\begin(array)(cccc|c) 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 7 & -9 & -25\end(array)\right) \begin(array) (l) I-2 /3\cdot III\\ \phantom(0) \\ \phantom(0)\\IV-7\cdot III\end(array)\pijl naar rechts\\ \pijl naar rechts\left(\begin(array)(cccc|c ) 1 & 0 & 0 & -1 & -5\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 0 & -39/2 & - 39\eind(matrix)\rechts). $$
Vierde stap
Laten we verder gaan met het op nul zetten van de vierde kolom. Het oplossende element bevindt zich in de vierde regel en is gelijk aan het getal $-\frac(39)(2)$.
$$ \left(\begin(matrix)(cccc|c) 1 & 0 & 0 & -1 & -5\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2 \\ 0 & 0 & 0 & -39/2 & -39\end(array)\right) \begin(array) (l) \phantom(0)\\ \phantom(0) \\ \phantom(0) \\IV:\left(-\frac(39)(2)\right) \end(array)\pijl rechts \left(\begin(array)(cccc|c) 1 & 0 & 0 & -1 & -5 \\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 0 & 1 & 2\end(array)\right) \begin(array) (l ) I+IV\\ II-5\cdot IV \\ III-3/2\cdot IV \\ \phantom(0) \end(array)\pijl naar rechts\\ \pijl naar rechts\left(\begin(array)(cccc |c) 1 & 0 & 0 & 0 & -3\\ 0 & 1 & 0 & 0 & -5\\ 0 & 0 & 1 & 0 & -1\\ 0 & 0 & 0 & 1 & 2\einde (matrix)\rechts). $$
De beslissing is voorbij. Het antwoord is: $x_1=-3$, $x_2=-5$, $x_3=-1$, $x_4=2$. Volledige oplossing zonder uitleg:

Antwoord: $x_1=-3$, $x_2=-5$, $x_3=-1$, $x_4=2$.
Voorbeeld nr. 3
SLAE $\left\(\begin(uitgelijnd) & x_1-2x_2+3x_3+4x_5=-5;\\ & 2x_1+x_2+5x_3+2x_4+9x_5=-3;\\ & 3x_1+4x_2+7x_3+4x_4 +14x_5=-1;\\ & 2x_1-4x_2+6x_3+11x_5=2;\\ & -2x_1+14x_2-8x_3+4x_4-7x_5=20;\\ & -4x_1-7x_2-9x_3-6x_4-21x_5=- 9. \end(aligned)\right.$ volgens de Gauss-Jordan-methode. Als het systeem onzeker is, geef dan de basisoplossing aan.
Soortgelijke voorbeelden worden besproken in het onderwerp “Algemene en basisoplossingen van SLAE’s”. In het tweede deel van het genoemde onderwerp dit voorbeeld opgelost met behulp van de Gaussische methode. We zullen het oplossen met behulp van de Gauss-Jordan-methode. We zullen de oplossing niet stap voor stap afbreken, aangezien dit in eerdere voorbeelden al is gedaan.
$$ \left(\begin(matrix)(ccccc|c) 1 & -2 & 3 & 0 & 4 & -5\\ 2 & 1 & 5 & 2 & 9 & -3\\ 3 & 4 & 7 & 4 & 14 & -1\\ 2 & -4 & 6 & 0 & 11 & 2\\ -2 & 14 & -8 & 4 & -7 & 20\\ -4 & -7 & -9 & -6 & -21 & -9 \end(array)\right) \begin(array) (l) \phantom(0) \\ II-2\cdot I\\ III-3\cdot I\\ IV-2\cdot I \\ V+2\cdot I\\VI+4\cdot I \end(array) \rightarrow \left(\begin(array)(ccccc|c) 1 & -2 & 3 & 0 & 4 & -5\ \\ 0 & 5 & -1 & 2 & 1 & 7\\ 0 & 10 & -2 & 4 & 2 & 14\\ 0 & 0 & 0 & 0 & 3 & 12\\ 0 & 10 & -2 & 4 & 1 & 10\\ 0 & -15 & 3 & -6 & -5 & -29 \end(array)\right) \begin(array) (l) \phantom(0) \\ II:5 \\ \ phantom(0)\\ \phantom(0)\\ \phantom(0) \\ \phantom(0)\end(array) \rightarrow \\ \left(\begin(array)(ccccc|c) 1 & - 2 & 3 & 0 & 4 & -5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 10 & -2 & 4 & 2 & 14\\ 0 & 0 & 0 & 0 & 3 & 12\\ 0 & 10 & -2 & 4 & 1 & 10\\ 0 & -15 & 3 & -6 & -5 & -29 \end(array)\right) \ begin (array) (l) I+2\cdot II \\ \phantom(0)\\ III-10\cdot II\\ IV:3\\ V-10\cdot II\\VI+15\cdot II \ end (array) \pijl naar rechts \left(\begin(array)(ccccc|c) 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\ 0 & 1 & -1/5 & 2 /5 & 1/5 & 7/5\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & -1 & - 4\\ 0 & 0 & 0 & 0 & -2 & -8 \end(array)\right). $$
Ik geloof dat een van de gemaakte transformaties nog steeds uitleg behoeft: $IV:3$. Alle elementen van de vierde regel zijn volledig deelbaar door drie, dus puur om redenen van vereenvoudiging hebben we alle elementen van deze regel in drieën gedeeld. De derde rij in de getransformeerde matrix werd nul. Laten we de nullijn doorstrepen:
$$ \left(\begin(array)(ccccc|c) 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & -1 & -4\\ 0 & 0 & 0 & 0 & -2 & -8 \end(array)\right) $$
Het is tijd voor ons om verder te gaan naar de derde stap, waarbij de elementen van de derde kolom opnieuw moeten worden ingesteld. Het diagonale element (derde rij) is echter nul. En het veranderen van de posities van de lijnen zal niets opleveren. We hebben de eerste en tweede regel al gebruikt, dus we kunnen ze niet aanraken. Maar het heeft geen zin om de vierde en vijfde regel aan te raken, omdat het probleem dat het oplossende element gelijk is aan nul niet zal verdwijnen.
In deze situatie kan het probleem op een uiterst eenvoudige manier worden opgelost. Kunnen we de derde colonne niet aan? Oké, laten we verder gaan met nummer vier. Misschien is in de vierde kolom het element van de derde rij niet gelijk aan nul. De vierde kolom kampt echter met hetzelfde probleem als de derde. Het derde rij-element in de vierde kolom is nul. En het opnieuw veranderen van de plaatsen van de lijnen levert niets op. Kunnen wij de vierde kolom ook niet verwerken? Oké, laten we verder gaan met nummer vijf. Maar in de vijfde kolom is het element van de derde rij niet eens nul. Het is gelijk aan één, wat behoorlijk goed is. Het oplossende element in de vijfde kolom is dus gelijk aan 1. Het oplossende element is geselecteerd, dus we zullen verdere transformaties van de Gauss-Jordan-methode uitvoeren:
$$ \left(\begin(array)(ccccc|c) 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & -1 & -4\\ 0 & 0 & 0 & 0 & -2 & -8 \end(array)\right) \begin(array) (l) I-22/5\cdot III \\ II-1/5\cdot III \\ \phantom(0)\\ IV+III\\ V+ 2 \cdot III \end(array) \rechterpijl \left(\begin(array)(ccccc|c) 1 & 0 & 13/5 & 4/5 & 0 & -99/5\\ 0 & 1 & -1 / 5 & 2/5 & 0 & 3/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 \end(array)\right) \rightarrow \\ \rightarrow\left|\text(Verwijder nul rijen)\right|\rightarrow \left(\begin(array)(ccccc|c) 1 & 0 & 13/5 & 4/5 & 0 & -99/5\\ 0 & 1 & -1/5 & 2/5 & 0 & 3/5\\ 0 & 0 & 0 & 0 & 1 & 4 \end(array)\ rechts )$$
We hebben de systeemmatrix en de uitgebreide systeemmatrix teruggebracht tot een stapsgewijze vorm. De rangen van beide matrices zijn gelijk aan $r=3$, d.w.z. je moet 3 basisvariabelen kiezen. Het aantal onbekenden is $n=5$, dus we moeten $n-r=2$ vrije variabelen kiezen. Sinds $r< n$, то согласно следствию из теоремы Кронекера-Капелли dit systeem is onzeker (dat wil zeggen heeft een oneindig aantal oplossingen). Om oplossingen voor het systeem te vinden, creëren we “stappen”:

Op de “stappen” staan elementen uit kolommen nr. 1, nr. 2, nr. 5. De basisvariabelen zijn dus $x_1$, $x_2$, $x_5$. De vrije variabelen zijn respectievelijk $x_3$, $x_4$. We zullen de kolommen nr. 3 en nr. 4, die overeenkomen met vrije variabelen, voorbij de lijn verplaatsen, waarbij we uiteraard niet vergeten hun tekens te veranderen.
$$ \left(\begin(array)(ccccc|c) 1 & 0 & 13/5 & 4/5 & 0 & -99/5\\ 0 & 1 & -1/5 & 2/5 & 0 & 3/5\\ 0 & 0 & 0 & 0 & 1 & 4 \end(array)\right)\pijl rechts \left(\begin(array)(ccc|ccc) 1 & 0 & 0 & -99/5 & -13/5 & -4/5\\ 0 & 1 & 0 & 3/5 & 1/5 & -2/5\\ 0 & 0 & 1 & 4 & 0 & 0\end(matrix)\rechts) . $$
Uit de laatste matrix verkrijgen we de algemene oplossing: $\left\(\begin(aligned) & x_1=-\frac(99)(5)-\frac(13)(5)x_3-\frac(4)(5 )x_4 \\ & x_2=\frac(3)(5)+\frac(1)(5)x_3-\frac(2)(5)x_4;\\ & x_3 \in R;\\ & x_4\ in R; \\ & x_5=4. \end(aligned)\right.$ We vinden de basisoplossing door de vrije variabelen gelijk aan nul te nemen, d.w.z. $x_3=0$, $x_4=0$:
$$ \left\(\begin(uitgelijnd) & x_1=-\frac(99)(5);\\ & x_2=\frac(3)(5);\\ & x_3=0;\\ & x_4= 0;\\ & x_5=4 \end(uitgelijnd)\right $$.
Het probleem is opgelost, het enige dat overblijft is het antwoord opschrijven.
Antwoord: Algemene oplossing: $\left\(\begin(uitgelijnd) & x_1=-\frac(99)(5)-\frac(13)(5)x_3-\frac(4)(5)x_4;\\ & x_2=\ frac(3)(5)+\frac(1)(5)x_3-\frac(2)(5)x_4;\\ & x_3 \in R;\\ & x_4\in R;\\ & x_5=4 .\end(uitgelijnd)\right.$, basisoplossing: $\left\(\begin(uitgelijnd) & x_1=-\frac(99)(5);\\ & x_2=\frac(3)(5) ;\\ & x_3=0;\\ & x_4=0;\\ & x_5=4 \end(uitgelijnd)\rechts.$.
4. Jordan - Gauss-methode.
Het schema met de keuze van het hoofdelement is dat de eis dat de diagonale elementen akk, waarin deling plaatsvindt tijdens het eliminatieproces, niet gelijk is aan nul, zal worden vervangen door een strengere: van alle elementen van de K-de kolom, selecteer de grootste in modulus en herschik de vergelijkingen zodat dit element op de plaats van het acc-element terechtkomt. De keuze van het hoofdelement en de daarmee samenhangende herschikking van rijen zijn noodzakelijk in gevallen waarin bij elke i-de stap acc = 0 of er zeer weinig acc zijn voor de overige elementen van de i-de kolom: bij het delen door zo’n “kleine” ” acc zal resulteren grote cijfers met grote absolute fouten, waardoor de oplossing sterk kan worden vertekend.
Hieronder staat een algoritme voor de volledige eliminatie van onbekenden of de Jordan-Gauss-methode. De essentie van de methode is dat, na de eerste vergelijking te hebben overwogen, deze een onbekende bevat met een coëfficiënt die verschilt van nul (hierna het oplossende element genoemd), en de eerste vergelijking door deze coëfficiënt deelt, met behulp van de eerste vergelijking, deze onbekende is uitgesloten van alle vergelijkingen behalve de eerste. Nadat je in de tweede vergelijking een onbekende hebt gekozen met een coëfficiënt die verschilt van nul en de tweede vergelijking erdoor deelt, elimineert het gebruik van de tweede andere onbekenden uit alle vergelijkingen behalve de tweede, enz., d.w.z. met behulp van één vergelijking elimineren ze één onbekende volledig. Het proces gaat door totdat alle vergelijkingen zijn gebruikt.
Zoals bekend kunnen systemen van lineaire algebraïsche vergelijkingen één oplossing hebben, meerdere oplossingen, of kunnen de systemen inconsistent zijn. Met elementaire transformaties van de elementen van de systeemmatrix worden deze gevallen als volgt onthuld:
1. In het proces van eliminaties linkerkant De eerste vergelijking van het systeem verdwijnt, en rechterkant gelijk aan een getal dat verschilt van nul. die. 02+=bc0.
Dit betekent dat het systeem geen oplossingen heeft, aangezien aan de I-de vergelijking niet kan worden voldaan door welke waarden van de onbekenden dan ook;
2. De linker- en rechterkant van de eerste vergelijking verdwijnen. Dit betekent dat de eerste vergelijking een lineaire combinatie is van de andere; elke oplossing die voor het systeem wordt gevonden, voldoet eraan en kan dus worden weggegooid. Het aantal onbekenden in het systeem meer kwantiteit vergelijkingen en daarom heeft zo’n systeem veel oplossingen;
3. Nadat alle vergelijkingen zijn gebruikt om de onbekenden te elimineren, wordt een oplossing voor het systeem verkregen.
Het uiteindelijke doel van de Jordan-Gauss-transformatie is dus het verkrijgen van een bepaald lineair systeem
| a11x1 + a12x2 + … + a1nxn = b1,n+1 |
| a21x1 + a22x2 + … + a2nxn = b2,n+1 |
| am1x1 + am2x2 + … + amnxn = bm.n+1 |
Hier zijn x1, x2, …, xn onbekenden die moeten worden bepaald. a11, a12, …, amn - coëfficiënten van het systeem - en b1, b2, ... bm - vrije termen - worden verondersteld bekend te zijn. De indices van de coëfficiënten (aij) van het systeem geven respectievelijk de getallen van de vergelijking (i) en de onbekende (j) aan waarbij deze coëfficiënt staat.
Systeem (1) wordt homogeen genoemd als al zijn vrije termen gelijk zijn aan nul (b1 = b2 = … = bm = 0), anders wordt het inhomogeen genoemd.
Systeem (1) wordt kwadratisch genoemd als het aantal m vergelijkingen gelijk is aan het aantal n onbekenden.
De oplossing voor systeem (1) is een reeks van n getallen c1, c2, ..., cn, zodat het vervangen van elke ci in plaats van xi in systeem (1) al zijn vergelijkingen in identiteiten verandert.
Systeem (1) wordt consistent genoemd als het ten minste één oplossing heeft, en inconsistent als het geen enkele oplossing heeft.
Gezamenlijk systeem type (1) kan een of meer oplossingen hebben.
Oplossingen c1(1), c2(1), …, cn(1) en c1(2), c2(2), …, cn(2) van een gezamenlijk systeem van type (1) worden verschillend genoemd als er minstens één van de gelijkheid wordt geschonden:
c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).
Een gelijktijdig systeem van de vorm (1) wordt definitief genoemd als het een unieke oplossing heeft; als ze er minstens twee heeft verschillende oplossingen, dan wordt het onbepaald genoemd. Als er meer vergelijkingen dan onbekenden zijn, wordt dit overbepaald genoemd.
Laten we het volgende stelsel vergelijkingen oplossen:

Laten we het schrijven als een 3x4-matrix, waarbij de laatste kolom een vrij lid is:

Laten we uitvoeren volgende stappen:
· Voeg aan regel 2 toe: -4 * Regel 1.
· Aan regel 3 toevoegen: -9 * Regel 1.

· Voeg aan regel 3 toe: -3 * Regel 2.
· Verdeel lijn 2 door -2

· Voeg aan regel 1 toe: -1 * Regel 3.
· Aan regel 2 toevoegen: -3/2 * Regel 3.

· Voeg aan regel 1 toe: -1 * Regel 2.

In de rechterkolom krijgen we de oplossing:
![]() .
.





Bij de methode van Newton wordt een versnelling van de convergentie van het benaderingsproces waargenomen. 5. Tangensmethode (methode van Newton) De tangensmethode, geassocieerd met de naam I. Newton, is een van de meest effectieve numerieke methoden voor het oplossen van vergelijkingen. Het idee van de methode is heel eenvoudig. Laten we het afgeleide punt x0 nemen en daarin de vergelijking schrijven van de raaklijn aan de grafiek van de functie f(x): y=f(x0)+ f ¢(x) (x-x0) (1.5) Grafieken...
Oplossingen uit numerieke rekenmethoden. Om de wortels van een vergelijking te bepalen, is kennis van de theorieën van Abel-, Galois-, Lie-, etc.-groepen en het gebruik van speciale wiskundige terminologie: ringen, velden, idealen, isomorfismen, etc. niet vereist. Om een algebraïsche vergelijking van de n-de graad op te lossen, heb je alleen het vermogen nodig om kwadratische vergelijkingen op te lossen en wortels te extraheren uit complex getal. Wortels kunnen worden bepaald door...





Wiskunde van trigonometrische substitutie en het testen van de effectiviteit van de ontwikkelde lesmethodologie. Fasen van het werk: 1. Ontwikkeling van een optionele cursus over het onderwerp: "Toepassing van trigonometrische substitutie voor het oplossen van algebraïsche problemen" met studenten in klassen met diepgaande studie wiskunde. 2. Het uitvoeren van het ontwikkelde keuzevak. 3. Een diagnostische test uitvoeren...





... “verschijnt” alleen tijdens het transformatieproces. We zullen de voor de hand liggende en “versluierde” van de nieuwe variabele bekijken op specifieke voorbeelden in het tweede hoofdstuk van dit werk. 2. Mogelijkheden om de methode van het vervangen van het onbekende te gebruiken bij het oplossen van algebraïsche vergelijkingen In dit hoofdstuk zullen we de mogelijkheden identificeren om de methode van het vervangen van het onbekende te gebruiken bij het oplossen van algebraïsche vergelijkingen in standaard en niet-standaard...
De Gauss-Jordan-methode is een van de bekendste en meest gebruikte methoden voor het oplossen van stelsels lineaire vergelijkingen. De matrixmethode en de methode van Cramer hebben als nadeel dat ze geen antwoord geven in het geval dat detA = 0, maar alleen een unieke oplossing bepalen als detA niet gelijk is aan 0. Een ander nadeel is dat de hoeveelheid wiskundige berekeningen binnen deze methoden neemt sterk toe met een toename van het aantal vergelijkingen. De Gauss-methode is vrijwel vrij van deze tekortkomingen.
Gauss-methode-algoritme
Commentaar op stap 2 van de Gaussiaanse methode. Een driehoekige matrix is een matrix waarin alle elementen die zich onder de hoofddiagonaal bevinden gelijk zijn aan nul.
- Op basis van het systeem van lineaire vergelijkingen stellen we een uitgebreide matrix van het systeem samen;
- We reduceren de matrix tot een “driehoekige” vorm;
- We bepalen de rangorde van de hoofd- en uitgebreide matrices, en op basis hiervan trekken we een conclusie over de compatibiliteit van het systeem en het aantal haalbare oplossingen;
- Als het systeem één enkele oplossing heeft, voeren we een omgekeerde substitutie uit en vinden deze als het systeem veel oplossingen heeft: we drukken de basisvariabelen uit via variabelen die willekeurige waarden kunnen aannemen;
Om de oorspronkelijke uitgebreide matrix te verkleinen tot driehoekig aanzicht We gebruiken de volgende twee eigenschappen van determinanten:
Eigenschap 1. De determinant zal zijn waarde niet veranderen als de overeenkomstige elementen van een parallelle rij (kolom) vermenigvuldigd met een willekeurig hetzelfde getal worden opgeteld bij alle elementen van een willekeurige rij (kolom) van de matrix.
Eigenschap 2. Wanneer twee kolommen of rijen van een matrix opnieuw worden gerangschikt, verandert de determinant van teken naar het tegenovergestelde, en absolute waarde de determinant blijft ongewijzigd.
Op basis van deze eigenschappen van determinanten zullen we een algoritme creëren voor het converteren van een matrix naar een driehoekige vorm:
- Beschouw regel i (beginnend bij de eerste). Als element a i i gelijk is aan nul, verander dan op plaatsen i-de en i+1e rijen van de matrix. Het teken van de determinant zal naar het tegenovergestelde veranderen. Als een 1 1 verschillend is van nul, ga dan naar de volgende stap;
- Voor elke lijn j, onder de i-de, vinden we de waarde van de coëfficiënt Kj =a j i /a i i;
- We herberekenen de elementen van alle rijen j hieronder huidige lijn i, met behulp van de overeenkomstige coëfficiënten volgens de formule: a j k new=a j k -K j *a ik k; Daarna keren we terug naar de eerste stap van het algoritme en overwegen we volgende regel
- , totdat we bij regel i=n-1 komen, waar n de dimensie van matrix A is
In de resulterende driehoekige matrix berekenen we het product van alle elementen van de hoofddiagonaal Pa i i , wat de bepalende factor zal zijn;
Met andere woorden, de essentie van de werkwijze kan als volgt worden geformuleerd. We moeten alle matrixelementen onder de hoofddiagonaal nul maken. Eerst krijgen we nullen in de eerste kolom. Om dit te doen, trekken we achtereenvolgens de eerste regel af, vermenigvuldigd met het getal dat we nodig hebben (zodat we bij het aftrekken nul krijgen in het eerste element van de regel), van alle onderliggende regels. Vervolgens doen we hetzelfde voor de tweede rij om nullen te krijgen in de tweede kolom onder de hoofddiagonaal van de matrix. En zo verder totdat we bij de voorlaatste regel komen. Laten we elk systeem van lineaire vergelijkingen associëren met uitgebreide matrix
, verkregen door toevoeging aan de matrix A kolom gratis leden: lineaire vergelijkingen met N onbekende soorten:
Deze methode ligt in het feit dat met behulp van elementaire transformaties een stelsel vergelijkingen wordt gereduceerd tot een gelijkwaardig stelsel vergelijkingen met een matrix van een bepaald type.
We voeren de volgende elementaire transformaties uit op de rijen van de uitgebreide matrix:
1. het herschikken van twee snaren;
2. een string vermenigvuldigen met een ander getal dan nul;
3. aan de ene string een andere string toevoegen, vermenigvuldigd met een bepaald getal;
4. een nulrij (kolom) weggooien.
Voorbeeld 2.11. Los stelsels van lineaire vergelijkingen op met behulp van de Jordan-Gauss-methode:
A) X 1 + X 2 + 2X 3 = -1
2X 1 - X 2 + 2X 3 = -4
4X 1 + X 2 + 4X 3 = -2
Oplossing: Laten we een uitgebreide matrix maken:
Iteratie 1
We selecteren het element als gidselement. Laten we de eerste kolom naar een enkele kolom converteren. Om dit te doen, voegt u de eerste regel toe aan de tweede en derde regel, vermenigvuldigd met respectievelijk (-2) en (-4). We krijgen de matrix:
Hiermee is de eerste iteratie voltooid.
Iteratie 2
Selecteer een gidselement. Sinds delen we de tweede regel door -3. Vervolgens vermenigvuldigen we de tweede regel met respectievelijk (-1) en 3, en voegen we deze toe met respectievelijk de eerste en derde regel. Laten we de matrix pakken
Iteratie 3
Selecteer een gidselement. Omdat we de derde regel delen door (-2). Laten we de derde kolom omzetten naar eenheid. Om dit te doen, vermenigvuldigt u de derde regel met respectievelijk (-4/3) en (-2/3) en telt u deze op bij respectievelijk de eerste en tweede regel. Laten we de matrix pakken
waar X 1 = 1, X 2 = 2, X 3 = -2.
Nadat de oplossing is voltooid, is het in de trainingsfase noodzakelijk om een controle uit te voeren door de gevonden waarden te vervangen door het oorspronkelijke systeem, dat in correcte gelijkheden zou moeten veranderen.
B) X 1 – X 2 + X 3 – X 4 = 4
X 1 + X 2 + 2X 3 + 3X 4 = 8
2X 1 +4X 2 + 5X 3 +10X 4 = 20
2X 1 – 4X 2 + X 3 – 6X 4 = 4
Oplossing: De uitgebreide matrix heeft de vorm:
Door elementaire transformaties toe te passen, krijgen we:
Bronsysteem equivalent volgende systeem vergelijkingen:
X 1 – 3X 2 – 5X 4 = 0
2X 2 + X 3 + 4X 4 = 4
Laatste twee rijen van de matrix A(2) zijn lineair afhankelijk.
Definitie. Matrixrijen e 1 , e 2 ,…, e m worden genoemd lineair afhankelijk, als er getallen zijn die niet tegelijkertijd gelijk zijn aan nul, zodat een lineaire combinatie van matrixrijen gelijk is aan de nulrij:
Waar 0 =(0, 0…0). De rijen van de matrix zijn lineair onafhankelijk, wanneer de combinatie van deze rijen gelijk is aan nul als en slechts als alle coëfficiënten gelijk zijn aan nul.
IN lineaire algebra heel belangrijk begrip matrix rang, omdat het speelt heel goed grote waarde bij het oplossen van stelsels van lineaire vergelijkingen.
Stelling 2.3 (over de rangorde van de matrix). De rangorde van een matrix is gelijk aan het maximale aantal lineair onafhankelijke rijen of kolommen, waardoor al zijn andere rijen (kolommen) lineair worden uitgedrukt.
Matrix-rang A(2) is gelijk aan 2, omdat erin maximaal aantal lineair onafhankelijke rijen is gelijk aan 2 (dit zijn de eerste twee rijen van de matrix).
Stelling 2.4 (Kronecker-Kapeli). Een systeem van lineaire vergelijkingen is alleen consistent als de rangorde van de matrix van het systeem gelijk is aan de rangorde van de uitgebreide matrix van dit systeem.
1. Als de rangorde van de matrix van een gezamenlijk systeem gelijk is aan het aantal variabelen, d.w.z. r = n, dan heeft het systeem een unieke oplossing.
2. Als de rangorde van de systeemmatrix kleiner is dan het aantal variabelen, d.w.z. R< n, то система неопределённая и имеет бесконечное множество решений.
In dit geval heeft het systeem vier variabelen en is de rangorde 2. Daarom heeft het een oneindig aantal oplossingen.
Definitie. Laten R< N, R variabelen X 1 , X 2 ,…, x r worden genoemd eenvoudig, als de determinant van een matrix uit de coëfficiënten ervan ( basis minor) verschilt van nul. Rest n-r variabelen worden genoemd vrij.
Definitie.Oplossing systeem waarin alles n-r vrije variabelen gelijk zijn aan nul wordt genoemd eenvoudig.
Gezamenlijk systeem kolom gratis leden: lineaire vergelijkingen met N variabelen ( M< n ) heeft een oneindig aantal oplossingen, waaronder een eindig aantal basisoplossingen die niet groter zijn dan , waarbij .
In ons geval, d.w.z. het systeem heeft niet meer dan 6 basisoplossingen.
De algemene oplossing is:
X1 = 3X 2 +5X 4
X3 = 4 – 2X 2 – 4X 4
Laten we basisoplossingen vinden. Om dit te doen, nemen we aan dat X 2 = 0, X 4 = 0, en vervolgens X 1 = 0, X 3 = 4. De basisoplossing heeft de vorm: (0, 0, 4, 0).
Laten we een andere basisoplossing verkrijgen. Om dit te doen nemen we X 3 en X 4 als vrije onbekenden. Laten we de onbekenden X 1 en X 2 uitdrukken via de onbekenden X 3 en X 4:
X 1 = 6 – 3/2X 2 – X 4
X 2 = 2 – 1/2X 3 – 2X 4.
Dan heeft de basisoplossing de vorm: (6, 2, 0, 0).
Voorbeeld 2.12. Los het systeem op:
X1 + 2X2 – X3 = 7
2X 1 – 3X 2 + X 3 = 3
4X 1 + X 2 – X 3 = 16
Oplossing: Transformeer de uitgebreide matrix van het systeem
De vergelijking die overeenkomt met de derde rij van de laatste matrix is dus tegenstrijdig - deze resulteerde in de onjuiste gelijkheid 0 = –1, daarom is dit systeem inconsistent. Deze conclusie kan ook worden verkregen door op te merken dat de rangorde van de systeemmatrix 2 is, terwijl de rangorde van de uitgebreide systeemmatrix 3 is.