Simple types. Simple and structured data types Simple data types

Structured data types define an ordered collection of scalar variables and are characterized by the type of their components.

Structured data types, unlike simple ones, define many complex values ​​with one common name. We can say that structural types determine a certain way of forming new types from existing ones.

There are several methods of structuring, each of which differs in the way it refers to individual components and, therefore, in the way it refers to the components included in the structure data. According to the method of organization and type of components in complex data types, the following varieties are distinguished:

§ regular type (arrays);

§ combined type (records);

§ file type (files);

§ multiple type (sets);

§ string type (strings);

§ in the Turbo Pascal language version 6.0 and older, an object type (objects) was introduced.

26)goto statement is an unconditional jump operator. It is used in the case when, after executing a certain statement, you need to go not to the statement following it, but to some other part of the program, marked with a special label. This label must be declared in the label description section of the program. The label can be either numeric, for example: goto 12, or contain alphabetic characters, for example: goto raschets.

The scope of the goto statement is only the block to which control was transferred. Transferring control to another block is impossible, since the specified label remains unchanged in the program.

An empty statement does not perform any action and does not contain any characters. Typically this operator is used to jump to the end of a local or global block. Especially in cases where you need to skip several statements, but not exit the block. To do this, a mark is placed before the reserved word “end” and a colon is required after it. For example:

gotoMetka; (Go to the end of the block)

Label: (An empty statement is marked with a label)

input - Read(<список_ввода>) and ReadLn(<список_ввода>).

The first of these commands reads all the data offered to it, leaving the cursor at the end of the last line of input, and the second, immediately after the end of the input, moves the cursor to the beginning of the next line. Otherwise, their actions are completely the same.

An input list is a sequence of variable names separated by commas. For example, using the command

ReadLn(k, x, c, s); (k: Byte; x: Real; c: Char; s: String)

the program can receive data from the keyboard for four variables at once, related to different data types.

Entered values ​​must be separated by spaces, and the entry must be completed by pressing the Enter key. Data entry ends at the moment when the last variable from the input list has received its value. Therefore, when entering data using the command above, you can press Enter four times - after each of the entered variables - or only once, after entering all four variables on one line (be sure to separate them with spaces).

The types of the entered values ​​must match the types of the specified variables, otherwise an error will occur. Therefore, you need to carefully monitor the correctness of the entered data.

In general, you can only enter data of basic types (with the exception of Boolean) from the keyboard. If the program still needs to get the value for a Boolean value from the console, it will have to act more cunningly: enter the specified symbol, and based on it, assign the corresponding value to a logical variable. For example:

WriteLn("Do you agree with this statement? y - yes, n - no");

ReadLn(c); (c: Char)

else WriteLn("Error!");

until (c = "n") or (c = "y");

Second exception: strings, although they are not a base type, are also allowed to be entered. A sign of the end of entering a line is pressing the Enter key, so all the variables following it must be entered on a new line.

Output - To display a message on the screen, use the Write(<список_вывода>) or WriteLn(<список_вывода>).

The first of them, having printed on the screen everything that was asked of it, will leave the cursor at the end of the output line, and the second will move it to the beginning of the next line.

Format - If you use the command given at the end of the previous paragraph to display information, the displayed characters will be “stitched together”. To prevent this from happening, you need to either take care of the spaces between the output variables:

WriteLn(a, " ", b, " ", c);

or set the output format for all (or at least some) variables:

WriteLn(a: 5, b, c: 20: 5);

The first number after the “:” sign indicates the number of positions allocated for the entire variable, and the second - for the fractional part of the number. The decimal point is also considered a separate character.

If the number is longer than the space allocated for it, the number of positions will be automatically increased. If the output number is shorter than the specified format, then several spaces will be added to it in front. This way you can produce output in nice, even columns, and also make sure that the variables do not merge.

For example, if a = 25, b = "x", and c = 10.5, then after executing the command WriteLn(a: 5, " ", b, c: 10: 5) the following will be written on the screen or in the file (underscores in in this case they serve only to visualize spaces):

25_x_ _10.50000

The format is especially important when displaying real variables. For example, if you do not specify a format, then the number 10.5 will be output as 1.0500000000E+0001. This format is called floating point notation.

If you specify only the total length of a real number, without specifying the length of the fractional part, then it will occupy the specified number of characters on the screen (if necessary, the corresponding number of spaces will be added in front), but will remain in floating point format. The minimum length for displaying real numbers is 10 (with the format _x.xE+yyyy). The first position is reserved for the “-” sign.

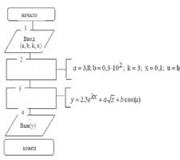
27) A linear structure algorithm (linear algorithm) – an algorithm in which blocks are executed sequentially one after another. This order of block execution is called natural .

Example. Calculate

Solution: The diagram of the linear structure algorithm looks like (Fig. 1.)

28)Simple and compound operators

An operator in a program is a single and indivisible sentence that performs an action. A typical simple operator is the assignment operator. Another example would be calling a procedure in a program. It is important that any operator implies an action (assignment, subroutine call, etc.). Blocks for defining variables, constants, types, and labels are not statements in this sense.

Two consecutive statements must be separated by a semicolon “;”.

Examples of simple operators:

a:= 10; b:= a*5; Write(a, b);

If some action is thought of as a single action, but is implemented by several different operators, then the latter can be represented as a compound operator.

A compound statement is a sequence of statements preceded by BEGIN and followed by END. The words BEGIN and END are often called operator brackets.

Example of a compound statement:

BEGIN
a:= 10;
b:+ a*5;
Write(a, b)
END;

A compound statement can contain any number of simple statements. It allows nesting, i.e. may contain other compound statements within it.

IMPORTANT: A compound operator is used in cases where the syntax of the Pascal language allows the use of only one operator, while the algorithm requires specifying a certain sequence of actions. In Pascal, all control structures (operators) do not distinguish between simple and compound operators: where there is a simple operator, you can also put a compound one.

30. loop with postcondition: Loops are used when you need to execute the same commands several times.

Let's consider the general form of a cycle with a postcondition:

[loop body];

Until< boolean expression>;

The advantages of this loop are the same as those of a loop with a precondition.

It is worth correctly understanding the essence of this loop: “Repeat the commands given in the body of the loop until the given condition is met (the logical expression is true).”

loop with precondition: Loops are used when you need to execute the same commands several times.

Let's look at the general form of a loop with a precondition:

While<логическое выражение> do[operator][;]

[loop body];

The main advantages of this cycle are:

1. The index can be changed not only in increments of plus or minus one, but for any amount, even not wholetype(of course, within reason), unlike a loop with a parameter.

2. In this cycle you can implement repetition commands up to certain condition- before logical expression.

It is worth correctly understanding the essence of this loop: “As long as this condition is met (or the logical expression is not false), we repeat the commands written in the body of the loop, otherwise we end the loop.”

Through a loop with a precondition, you can implement a loop with a parameter, followed by one “but” - in practice it is better to use “for”.

Related information.

The structural algorithmization method is one of the systematic methods for developing algorithms. It is based on a visual representation of algorithms in the form of sequences of control structural fragments.

Each algorithm consists of elementary steps that can be combined into certain algorithmic structures: linear (sequential), branching , cyclical .

Definition 1

Linear is an algorithm design implemented as a sequence of actions (steps), with each action (step) performed only 1 time, after each action (step) the action (step) is increased by 1 until the value is greater than the final parameter of the algorithm .

Linear processes are represented using linear algorithms. Algorithms of this type are used to describe a generalized solution to problems in the form of sequences of modules.

Definition 2

Branching (branching) call an algorithmic design that provides a choice between 2 solutions depending on the values ​​of the input data.

There are two types of branches: incomplete (if something) And complete (if-then-else). Using full branching, you can organize 2 branches in the algorithm ( That or otherwise), each of which will lead to a common point of their merger, the algorithm will be executed regardless of which path the solution took. In the presence of incomplete branching, some actions of the algorithm are assumed on only one branch ( That), since the second one is missing, there is no need to perform any action for one of the check results; control will immediately pass to the merge point. There are 4 basic variants of the branching structure:

1. Incomplete branching type "if-then ", under which all actions will be carried out if the condition is true.
2. Full type branching "if - then - otherwise" , in which 2 actions will be performed depending on the truth of the condition.
3. Branching with type selection "That" , in which action 1 will be performed under condition 1, action 2 under condition 2, etc.
4. Branching with type selection "otherwise" , under which, under condition 1, action 1 will be performed, under condition 2, action 2, etc., and otherwise all other actions will be performed.

Below are block diagrams of branching algorithms.

Definition 3

Cyclic (or cycle) is an algorithm design in which a certain group of consecutive actions (steps) is performed several times depending on the conditions of the problem and input data.

Definition 4

Such a group of repeated actions at each step of the cycle is called body of the loop .

Any cyclic structure contains elements of a branching structure of the algorithm.

There are 3 types of cyclic algorithms:

• loop with parameter (arithmetic loop);
• loop with precondition;
• a loop with a postcondition (the last two are called iterative).

Arithmetic loop

In a cycle of this type, the number of steps is uniquely determined by the rule for changing the parameter, specified using its initial and final values, as well as the step of its change. That is, at each step of the cycle, the value of the parameter changes according to the step of the cycle until it reaches a value equal to the final value of the parameter.

Loop with precondition

In this loop, the number of steps is not determined in advance; it depends on the input data. In this cyclic structure, the value of the conditional expression (condition) before executing the next step of the cycle is first checked. If the conditional expression is true, the body of the loop will be executed. After which the condition will be checked again. These actions will be repeated until the value of the conditional expression becomes false, then the loop will end.

The peculiarity of this type of loop is that if the value of the conditional expression is initially false, the body of the loop will not be executed at all.

Loop with postcondition

In this cyclic construction, as in the previous one, the number of repetitions of the loop body is not determined in advance; it will depend on the input parameters. A distinctive feature of a loop with a precondition is that the body of the loop with a postcondition will in any case be executed at least once and only after that the condition will be checked. In this construction, the body of the loop is executed until the value of the conditional expression is false. Once it becomes true, command execution will stop.

In real problems, as a rule, there are any number of cycles.

Below are block diagrams of cyclic algorithms.

Data types: simple and structured

Real data processed by the program includes integer and real numbers, logical values ​​and symbols. They belong to simple data types and are called basic. All data processed by a computer is stored in its memory cells, each of which has its own address. In programming languages, there are variables that allow you to ignore the addresses of memory cells and access them using a name (identifier).

Definition 5

Variable is a named object (memory cell) that changes its value.

The variable name indicates the value, but the address and method of storing it remain hidden from the programmer. In addition to the name and value, variables have their own type, which helps determine what type of information is in memory.

The variable type is specified by:

• the method used for recording information into memory cells;
• the required amount of memory to store it.

For each type, the amount of memory is determined so that any value from the allowable range of values ​​for this type can be placed in it.

Definition 6

Variables that are present in the program throughout the entire period of its operation are called static .

Definition 7

Variables that are created and destroyed at different stages of program execution are called dynamic .Definition 10

Array They call an ordered set of quantities of the same type that have a common name and serial numbers of elements (indices).

The elements of an array are stored in the computer's memory nearby, unlike single elements. Arrays are distinguished by the number of element indices.

A one-dimensional array is characterized by the presence of only one index for each element. Examples of one-dimensional arrays are geometric and arithmetic sequences, which define finite series of numbers.

Definition 11

The number of elements in an array is called dimension .

For a one-dimensional array, its dimension is written next to the name in parentheses.

Elements of a one-dimensional array are entered element by element, in the order necessary to solve a specific problem. If it is necessary to enter the entire array, the elements are entered in ascending index order.

A data type defines a set of valid values ​​and a set of valid operations.

Simple types.

Simple types are divided into ORDINAL and REAL.

1. ORDERAL TYPES , in turn, there are:

a) whole

Pascal defines 5 integer types, which are defined depending on the sign and value that the variable will take.

b) logical

The name of this type is BOOLEAN. Boolean values ​​can be one of the Boolean constants: TRUE (true) or FALSE (false).

c) symbolic

The name of this type is CHAR - occupies 1 byte. The value of a character type is the set of all PC characters. Each character is assigned an integer in the range 0…255. This number serves as a code for the internal representation of the symbol.

2. REAL TYPES .

Unlike ordinal types, whose values ​​are always mapped to a series of integers and are therefore represented absolutely precisely in PC, the values ​​of real types define an arbitrary number only with some finite precision depending on the internal format of the real number.

STRUCTURED TYPES

Structured data types define an ordered collection of scalar variables and are characterized by the type of their components.

Structured data types, unlike simple ones, define many complex values ​​with one common name. We can say that structural types determine a certain way of forming new types from existing ones.

There are several structuring methods. According to the method of organization and type of components in complex data types, the following varieties are distinguished: regular type (arrays); combined type (records); filetype(files); multiple type(s); string type(strings); in the Turbo Pascal language version 6.0 and older, an object type (objects) was introduced.

Unlike simple data types, structured type data is characterized by the multiplicity of elements that form this type, i.e. a variable or constant of a structured type always has multiple components. Each component, in turn, can belong to a structured type, i.e. nesting of types is possible.

1. Arrays

Arrays in Turbo Pascal are in many ways similar to similar data types in other programming languages. A distinctive feature of arrays is that all their components are data of the same type (possibly structured). These components can be easily organized and any one of them can be accessed simply by specifying a serial number.

The array description is specified as follows:

<имя типа>= array[<сп.инд.типов>] of<тип>

Here<имя типа>- correct identifier;

Array, of – reserved words (array, from);

<сп.инд.типов>- a list of one or more index types, separated by commas; square brackets framing the list are a syntax requirement;

<тип>- any type of Turbo Pascal.

Any ordinal types can be used as index types in Turbo Pascal, except LongInt and range types with the base type LongInt.

The depth of nesting of structured types in general, and therefore of arrays, is arbitrary, so the number of elements in the list of type indexes (array size) is not limited, however, the total length of the internal representation of any array cannot be more than 65520 bytes.

2. Records

A record is a data structure consisting of a fixed number of components called record fields. Unlike an array, the components (fields) of a record can be of different types. To make it possible to refer to one or another component of a record, the fields are named.

The structure of a post type declaration is:

< Nametype>=RECORD< joint venture. fields>END

Here<имя типа>- correct identifier;

RECORD, END – reserved words (record, end);

<сп.полей>- list of fields; is a sequence of sections of a record separated by a semicolon.

3. Sets

Sets are a set of objects of the same type that are logically connected to each other. The nature of the connections between objects is only implied by the programmer and is in no way controlled by Turbo Pascal. the number of elements included in a set can vary from 0 to 256 (a set that does not contain elements is called empty). It is the inconstancy of the number of its elements that sets differ from arrays and records.

Two sets are considered equivalent if and only if all their elements are the same, and the order of the elements of the set is indifferent. If all the elements of one set are also included in another, the first set is said to be included in the second.

The description of the set type is:

< Nametype> = SET OF< bases. type>

Here<имя типа>- correct identifier;

SET, OF – reserved words (set, from);

<баз.тип>- the base type of set elements, which can be any ordinal type except WORD, INTEGER and LONGINT.

To define a set, the so-called set constructor is used: a list of specifications of the elements of the set, separated by commas; the list is surrounded by square brackets. Element specifications can be constants or expressions of a base type, as well as a range type of the same base type.

4. Files

A file is understood as either a named area of ​​external memory of a PC, or a logical device - a potential source or receiver of information.

Any file has three characteristic features

it has a name, which allows the program to work with several files simultaneously.

it contains components of the same type. The component type can be any Turbo Pascal type, except files. In other words, you cannot create a “file of files.”

the length of the newly created file is not specified in any way when it is declared and is limited only by the capacity of external memory devices.

A file type or file type variable can be specified in one of three ways:

< Name>= FILE OF< type>;

< Name>=TEXT;

<имя>= FILE;

Here<имя>- file type name (correct identifier);

FILE, OF – reserved words (file, from);

TEXT – name of the standard text file type;

<тип>- any type of Turbo Pascal, except files.

Depending on the method of declaration, three types of files can be distinguished:

· typed files (set by the FILE OF... clause);

· text files (defined as TEXT type);

· untyped files (defined by the FILE type).

About converting Pascal's numeric data types

In Pascal, implicit (automatic) conversions of numeric data types are almost impossible. An exception is made only for the integer type, which is allowed to be used in expressions of type real. For example, if the variables are declared like this:

Var X: integer; Y: real;

then the operator

will be syntactically correct, although there is an integer expression to the right of the assignment sign and a real variable to the left, the compiler will convert numeric data types automatically. The reverse conversion automatically from the real type to the integer type is impossible in Pascal. Let's remember how many bytes are allocated for variables of type integer and real: 2 bytes of memory are allocated for the integer data type integer, and 6 bytes for real. There are two built-in functions for converting real to integer: round(x) rounds a real x to the nearest integer, trunc(x) truncates a real by discarding the fractional part.

Simple types include ordinal, real, and datetime types.

Ordinal types are different in that they each have a finite number of possible values. These values ​​can be ordered in a certain way (hence the name of the types) and, therefore, each of them can be associated with some integer - the ordinal number of the value.

Real types, strictly speaking, also have a finite number of values, which is determined by the format of the internal representation of a real number. However, the number of possible values ​​of real types is so large that it is not possible to associate an integer (its number) with each of them.

The datetime type is designed to store date and time. In fact, it uses the real format for these purposes.

Ordinal types

Ordinal types include (see Figure 1.1) integer, logical, character, enumerated, and range types. The Ord(x) function can be applied to any of them, which returns the ordinal number of the value of the expression X.

Rice. 1.1

For integer types, the function ord(x) returns the value of x itself, i.e. Ord(X) = x for x belonging to any integer type. Applying Ord(x) to boolean, character, and enumeration types produces a positive integer in the range 0 to 1 (boolean), 0 to 255 (character), 0 to 65535 (enumeration). A range type retains all the properties of the underlying ordinal type, so the result of applying the ord(x) function to it depends on the properties of that type.

You can also apply functions to ordinal types:

pred(x) - returns the previous value of the ordinal type (the value that corresponds to the ordinal number ord(x) -1, i.e. ord(pred(x)) = ord(x) - 1;

succ(x) - returns the next value of the ordinal type, which corresponds to the ordinal number ord(x) +1, i.e. ord(Succ(x)) = ord(x) + 1.

For example, if a program defines a variable

then the function PRED(c) will return the character "4", and the function SUCC(c) will return the character "6".

If we imagine any ordinal type as an ordered set of values ​​increasing from left to right and occupying a certain segment on the number axis, then the function pred(x) is not defined for the left end, and succ (x) is not defined for the right end of this segment.

Whole types. The range of possible values ​​of integer types depends on their internal representation, which can be one, two, four, or eight bytes. In table 1.1 shows the names of integer types, the length of their internal representation in bytes and the range of possible values.

Table 1.1 - Integer types

The LongWord and Int64 types were first introduced in version 4, but the Smallint and Cardinal types were absent from Delphi 1. The integer type for this version occupies 2 bytes and has a value range from -32768 to +32767, i.e., the same as Smallint.

When using procedures and functions with integer parameters, you should be guided by the “nesting” of types, i.e. wherever word can be used, Byte is allowed (but not vice versa), Longint “includes” Smallint, which, in turn, includes Shortint.

The list of procedures and functions applicable to integer types is given in table. 1.2. The letters b, s, w, i, l denote expressions of type Byte, Shortint, Word, Integer and Longint, respectively,

x is an expression of any of these types; the letters vb, vs, vw, vi, vl, vx denote variables of the corresponding types. An optional parameter is indicated in square brackets.

Table 1.2 - Standard procedures and functions applicable to entire types

When operating with integers, the result type will correspond to the type of the operands, and if the operands are of different integer types, the general type that includes both operands. For example, when working with shortint and word, the common type will be integer. In the default setting, the Delphi compiler does not produce code to check whether a value is out of range, which can lead to misunderstandings.

Logical types. Boolean types include Boolean, ByteBool, Bool, wordBool and LongBool. In standard Pascal, only the Boolean type is defined, the remaining logical types are introduced in Object Pascal for compatibility with Windows: the Boolean and ByteBool types occupy one byte each, Bool and WordBool - 2 bytes, LongBool - 4 bytes. Boolean values ​​can be one of the pre-declared constants False or True.

Since the Boolean type is an ordinal type, it can be used in a loop statement of a countable type. In Delphi 32 for Boolean value

Ord(True) = +1, while for other types (Bool, WordBool, etc.)

Ord(True) = -1, so these kinds of operators should be used with caution! For example, for Delphi 6, the executable showMessage (" --- ") statement in the following for loop will not be executed even once:

for L:= False to True do

ShowMessage("--);

If you change the type of the loop parameter L in the previous example to Boolean, the loop will run and the message will appear on the screen twice. [For Delphi versions 1 and 2 ord (True) =+1 for any boolean type.]

Character type. The value of a character type is the set of all PC characters. Each character is assigned an integer in the range 0...255. This number serves as the code for the internal representation of the symbol; it is returned by the ord function.

For encoding in Windows, the ANSI code is used (named after the American National Standard Institute, the American standardization institute that proposed this code). The first half of PC characters with codes 0... 127 corresponds to Table 1.3. The second half of characters with codes 128...255 varies for different fonts. Standard Windows fonts Arial Cyr, Courier New Cyr and Times New Roman use the last 64 codes (from 192 to 256) to represent Cyrillic characters (without the letters “ё” and “Ё”): “A”... “Z” are encoded values ​​192..223, “a”... “i” - 224...255. The symbols “Ё” and “е” have codes 168 and 184, respectively.

Table 1.3 - Character encoding in accordance with the ANSI standard

Characters with codes 0...31 refer to service codes. If these codes are used in the program's character text, they are considered whitespace.

The char type applies relational operations, as well as built-in functions:

Сhar (в) - function of type char; converts an expression of type Byte into a character and returns it with its value;

UpCase(CH) - function of type char; returns a capital letter if сн is a lowercase Latin letter, otherwise returns the symbol сн itself (for Cyrillic it returns the original character).

Enumerated type. An enumerated type is specified by an enumeration of the values ​​it can receive. Each value is named by some identifier and is located in a list surrounded by parentheses, for example:

colors = (red, white, blue);

The use of enumerated types makes programs more visual.

The correspondence between the values ​​of an enumerated type and the ordinal numbers of these values ​​is established by the enumeration order: the first value in the list receives the ordinal number 0, the second - 1, etc. The maximum cardinality of an enumerated type is 65536 values, so in fact the enumerated type defines some subset of the entire type word and can be considered as a compact declaration of a group of integer constants with values ​​0, 1, etc.

Using enumerated types increases the reliability of programs by allowing you to control the values ​​that corresponding variables receive. Object Pascal allows the reverse conversion: any expression of a Word type can be converted to a value of an enum type, as long as the value of the integer expression does not exceed the cardinality of that type. This conversion is achieved by using an automatically declared function with the name of the enumerated type.

Type-range. A range type is a subset of its base type, which can be any ordinal type except a range type.

A range type is defined by the boundaries of its values ​​within the base type:

<мин.знач.>..<макс.знач.>

Here<мин. знач. >- minimum value of type-range;<макс. знач. >- its maximum value.

The range type does not have to be described in the type section, but can be specified directly when declaring the variable.

When determining a range type, you must follow the following rules:

two “..” characters are treated as one character, so spaces between them are not allowed; the left border of the range should not exceed its right border.

A range type inherits all the properties of its base type, but with the limitations of its lower power. In particular, if a variable is defined.

The Object Pascal standard library includes two functions that support working with range types:

High(x) - returns the maximum value of the range type to which variable x belongs;

Low (x) - returns the minimum value of the range type.

Real types

Unlike ordinal types, whose values ​​are always mapped to a series of integers and are therefore represented absolutely precisely in PC, the values ​​of real types define an arbitrary number only with some finite precision depending on the internal format of the real number.

Table 1.4 - Real types

In previous versions of Delphi 1...3, the Real type occupied 6 bytes and had a range of values ​​from 2.9*10-39 to 1.7*1038. In versions 4 and 5, this type is equivalent to the Double type. If you want (for compatibility reasons) to use 6-byte Reals, you need to specify a compiler directive (SREALCOMPATIBILITY ON).

As can be seen from table. 1.4, a real number in Object Pascal occupies from 4 to 10 contiguous bytes and has the following structure in PC memory.

Here s is the sign digit of the number; e - exponential part; contains binary order; m is the mantissa of the number.

The mantissa m has a length from 23 (for single) to 63 (for Extended) binary digits, which ensures an accuracy of 7...8 for single and 19...20 for Extended decimal digits. The decimal point (comma) is implied before the left (most significant) digit of the mantissa, but when operating on a number, its position is shifted to the left or right in accordance with the binary order of the number stored in the exponential part, therefore operations on real numbers are called floating point (comma) arithmetic .

Note that the arithmetic coprocessor always processes numbers in the Extended format, and the three other real types in this case are obtained by simply truncating the results to the required size and are used mainly to save memory.

A special position in Object Pascal is occupied by the comp and Currency types, which are treated as real numbers with fractional parts of a fixed length: in comp the fractional part has a length of 0 digits, i.e., it is simply absent, in currency the length of the fractional part is -4 decimal places. In fact, both types define a large signed integer that stores 19...20 significant decimal digits (internally they occupy 8 contiguous bytes). At the same time, comp and currency expressions are fully compatible with any other real types: all real operations are defined on them, they can be used as arguments to mathematical functions, etc. The most suitable area of ​​application for these types is accounting calculations.

Composite, or structural, data types, in contrast to simple ones, define sets of complex values ​​with one common name. We can say that structural types define a certain way of creating new data types based on existing ones. Thus, it is possible to form data structures of arbitrary complexity, thereby making it possible to achieve an adequate representation in the program of the data with which it operates.

There are several methods of structuring, each of which differs in the way it refers to individual components and, therefore, in the way it refers to the components included in the structure data. According to the method of organization and type of components in complex data types, the following varieties are distinguished:

• regular type (arrays);
• combined type (records);
• filetype(files);
• multiple type(s);
• string type(strings);
• object type (objects).

Unlike simple data types, structured type data is characterized by the multiplicity of elements that form this type, i.e. a variable or constant of a structured type always has multiple components. Each component, in turn, can belong to a structured type, i.e. nesting of types is possible.

Literature

1. Popov V.B. Pascal and Delphi. Self-instruction manual - St. Petersburg: Peter, 2004. - 544 pp.: ill.